
pис. 1
Лабораторная работа №11
Разложение функции в ряд
Цель:
1. Разложение функций в ряды Тэйлора и Маклорена
Еще одна распространенная математическая задача - разложение заданной аналитической функции в степенной ряд Тэйлора относительно некоторой точки с абсциссой xo (при xo=0 он становится рядом Маклорена). Такой ряд зачастую проще самой функции, он дает единообразное представление для разлагаемых в него функций в виде обычного степенного многочлена. Большинство достаточно гладких функций, не имеющих разрывов в области разложения, довольно точно воспроизводятся рядом Тэйлора.
Для разложения в ряд используется следующая команда системы Mathematica:
Series [ f, { x ,xo, n} ] - выполняет разложение в степенной ряд функции f в окрестности точки x=xo по степеням (x-xo)n.

Представление функции степенным рядом всегда содержит некоторую остаточную погрешность. В соответствии с принятой математической символикой она обозначается как O(x)n с показателем степени n, указывающим на порядок погрешности. Погрешность возрастает с ростом отклонения от узловой точки. На рис.2 представлены графики экспоненты, построенные по аналитическому выражению и по разложению в ряд Тэйлора. Хорошо заметно расхождение за пределами области, примыкающей к опорной точке функции.

2. Удаление члена с остаточной погрешностью ряда
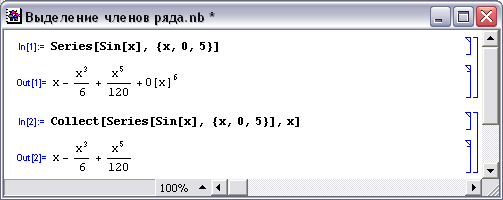
В некоторых случаях вывод члена с остаточной погрешностью ряда нежелателен, например, если разложение в ряд используется для последующих операций, таких как построение по ряду приближенного графика функции. На рис.3 показан способ выделения требуемого числа членов ряда.
Задание: Разложите данные ниже функции в степенные ряды по степеням x:
y=Ln ( x + √(1 + x2) )
y=arcsin x
y=(1+x) arctg x